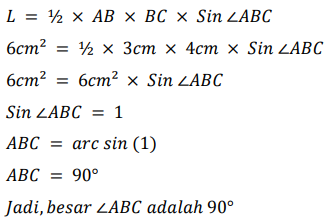.png) TRIGONOMETRI 1
TRIGONOMETRI 1Ada 6 jenis perbandingan trigonometri, yaitu sinus, kosinus, tangen, cosekan, sekan, dan kotangen. Perbandingan yang dimaksud adalah pada panjang sisi segitiga siku-siku.
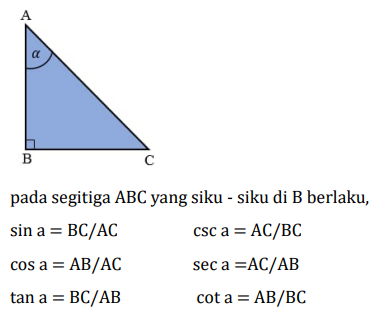
Contoh:


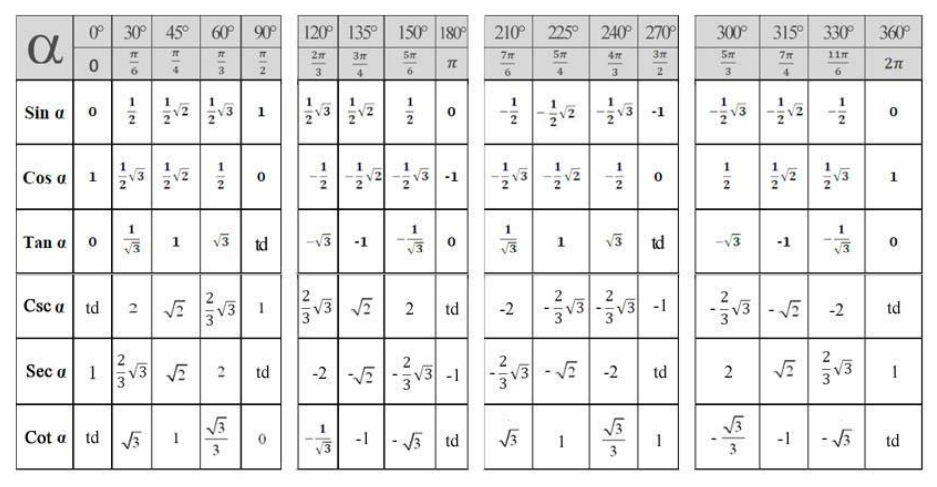
Adalah sudut-sudut yang memiliki nilai sinus, kosinus, dan tangen yang dapat dinyatakan dalam bentuk bilangan bulat atau pecahan sederhana.
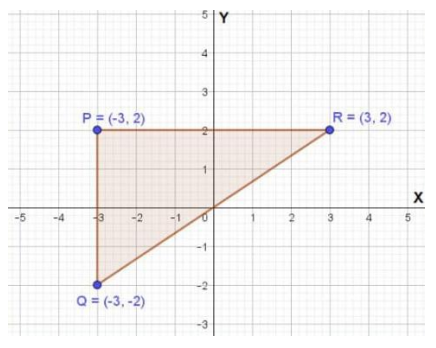
Contoh:
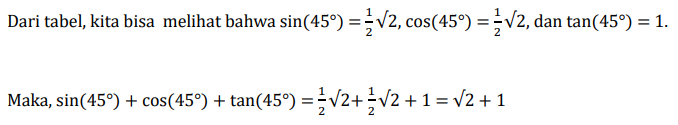

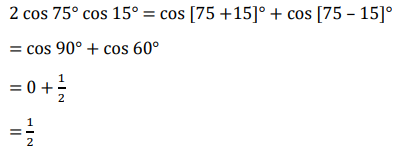

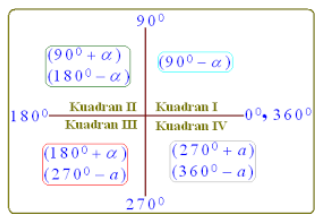
Konsep Dasar


Contoh:
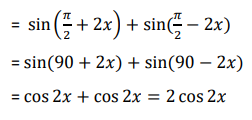

Adalah suatu pernyataan matematis yang menunjukkan kesetaraan antara dua ekspresi trigonometri. Pada dasarnya, identitas ini memungkinkan kita untuk mengubah atau menjelaskan satu fungsi trigonometri di sisi kiri atau kanan persamaan sehingga menghasilkan bentuk akhir yang sama dengan sisi lainnya.
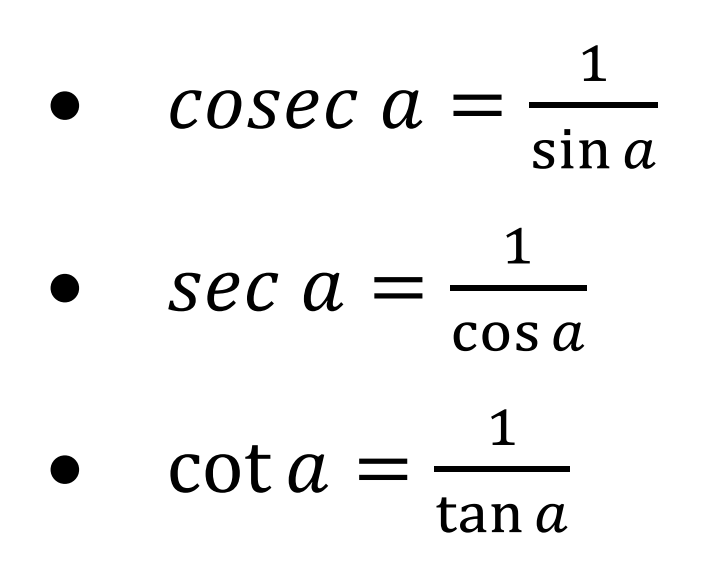
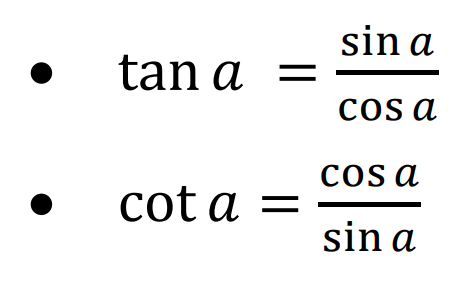

Contoh:
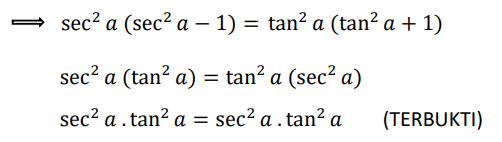
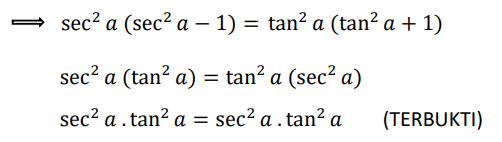
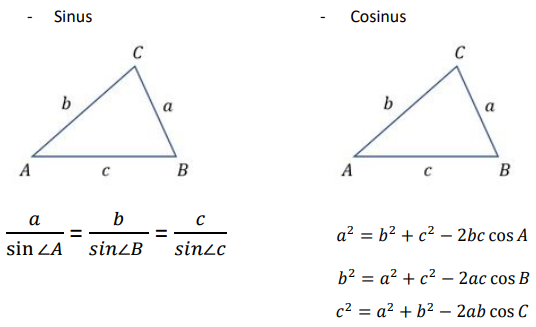
Contoh: