Kata Pengantar
Puji dan syukur saya panjatkan ke hadirat Tuhan Yang Maha Esa karena atas rahmat dan karunia-Nya, saya dapat menyelesaikan website ini yang berjudul "Teorema L'Hôpital". Website ini disusun untuk memahami lebih dalam mengenai konsep limit, khususnya dalam menyelesaikan bentuk tak tentu menggunakan metode L'Hôpital.
Di sini saya membahas pengertian Teorema L'Hôpital, pembuktiannya, serta beberapa contoh penerapannya dalam menyelesaikan limit yang berbentuk 0/0 atau ∞/∞ .
Semoga ilmu yang terdapat di sini dapat memberikan manfaat bagi kita semua.
Aturan L'Hopital
Aturan L'Hopital (L'Hopital's rule) diucapkan sebagai "lopeetals rule" dan aturan ini merupakan aturan yang sangat penting dalam kalkulus yang digunakan untuk mengevaluasi limit ganjil yang menghasilkan bentuk tak tentu (seperti 0/0, ∞/∞, dst). Jenis limit ini tidak dapat dihitung dengan substitusi langsung limit dan/atau dapat dievaluasi tetapi menggunakan prosedur yang sangat panjang.
Mari kita lihat Aturan L'Hopital beserta pernyataan, bukti, dan contohnya.
Sebelum itu, mari kita lihat contoh dari limit:
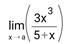
Cara menghitung limit sendiri adalah dengan memasukkan atau mensubtitusikan nilai a pada variabel x, hasil dari limit tersebut adalah:
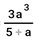
Tetapi ada suatu kondisi ketika hasil yang didapatkan dari limit adalah 0/0 atau ∞/∞, contoh:
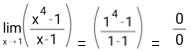
Limit yang memiliki hasil 0/0 atau ∞/∞ disebut sebagai limit tak tentu. Salah satu cara untuk menjawab soal limit tak tentu adalah dengan menggunakan aturan L’Hopital.
Aturan L’Hopital memberi tahu kalau misalnya ada limit tak tentu dengan hasil 0/0 atau ∞/∞, kamu bisa menyelesaikan limit tersebut dengan menurunkan si pembilang dan penyebut dari fungsi limitnya. Setelah itu, nanti substitusi nilai ‘a’ ke variabel ‘x’ ketika dimasukkan ke dalam fungsi yang udah diturunkan, jadinya bisa memperoleh nilai limit yang pantas.
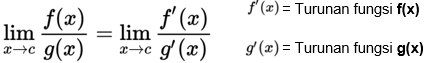
Masih ingat tidak dengan konsep turunan? Kalau begitu, ayo kita bahas sekilas.

Kembali lagi dari soal di atas, jadi:
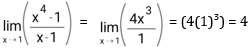
Pembuktian Aturan L'Hopital
Misalkan 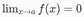 dan
dan 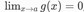 , serta f dan g terdiferensialkan di sekitar a, dengan
, serta f dan g terdiferensialkan di sekitar a, dengan 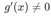 . Kita gunakan Teorema Cauchy tentang nilai rata-rata.
. Kita gunakan Teorema Cauchy tentang nilai rata-rata.
Teorema MVT versi Cauchy menyatakan bahwa jika f(x) dan g(x) terdiferensialkan pada interval (a, x), maka ada suatu c ∈ (a,x) sehingga:
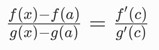
Karena f(a) = g(a) = 0, maka:
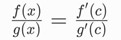
Jika x → a maka c → a karena terletak di antara a dan x. Dengan asumsi ada 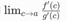 , maka:
, maka:
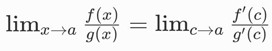
Karena c hanya variabel antara, kita dapat menggantinya dengan x, sehingga:
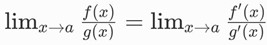
Pembuktian selesai…
L'Hopital 3gonome3
Fungsi bisa diturunkan terus-menerus sampai mencapai hasil yang diinginkan Bagaimana? Sangat mudah dipahami bukan? Tetapi sayangnya tidak semua soal limit akan semudah itu dikerjakan.
Contoh:
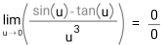
Bagaimana cara mengerjakannya? Tentu memasukkan rumus L'Hopital tidak akan langsung manjur. Oleh karena itu, ada beberapa sifat-sifat turunan yang wajib kalian ingat:

Contoh Soal
Berikut contoh soal yang bisa diselesaikan dengan L:Hopital dan sifat di atas:
1.
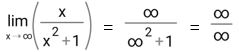
Hasil tersebut tidak bisa diterima, maka kita gunakan aturan L'Hopital
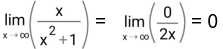 ← Ini jawaban yang benar
← Ini jawaban yang benar
2.
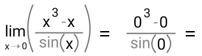
Hasil tersebut tidak bisa diterima, maka kita gunakan aturan L'Hopital
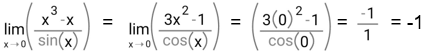
3. Seorang peneliti mengamati pertumbuhan populasi bakteri di laboratorium. Ia menemukan bahwa jumlah bakteri setelah t jam dapat dinyatakan oleh fungsi
P(t) = t² + 3t − 4
Untuk mengetahui laju pertumbuhan populasi bakteri dengan tepat, peneliti menghitung perubahan rata‐rata populasi dalam interval waktu yang sangat kecil, yaitu dengan menghitung fungsi 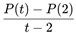 .
.
Hitung nilai dari fungsi tersebut untuk menentukan laju pertumbuhan instan populasi bakteri pada saat disekitar 2 jam
Jawaban:

Latihan Soal
-
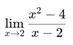
-
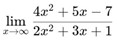
-
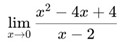
-
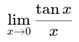
-
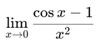
-
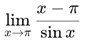
-
Seorang insinyur memantau beban yang bekerja pada sebuah struktur bangunan. Beban (dalam satuan Newton) pada waktu t (dalam jam) diberikan oleh fungsi:
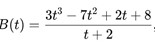 dengan t ≥ −2 (agar penyebut tidak sama dengan nol).
dengan t ≥ −2 (agar penyebut tidak sama dengan nol).
Untuk menentukan laju perubahan beban tepat pada saat t = 1 jam, insinyur tersebut menghitung perubahan rata‑rata beban dalam interval waktu yang sangat kecil melalui limit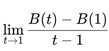 .
.
Selesaikan limit tersebut untuk menentukan nilai laju perubahan beban pada saat t = 1 jam!
Kirimkan pesan untuk tanya pembahasan.

