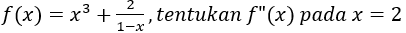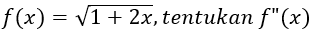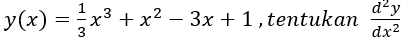Pengantar
Selamat datang di materi Turunan Kedua. Pada Turunan Kedua ini, materi yang akan kita pelajari lumayan simple. Hal ini karena turunan kedua hanya melanjutkan hasil dari turunan pertama yang diturunkan lagi, simple gak? GAK, karena belum dicoba, yuk kenal lebih lanjut sini sama Om!
Definisi
Secara definisi, turunan kedua adalah kegiatan melakukan turunan kembali dari f(x) hasil turunan pertama. Gampangnya gini, biasanya kita melakukan turunan hanya satu kali, sedangkan yang ini kita lakukan dua kali (turunan dari turunan pertama).
Rumus
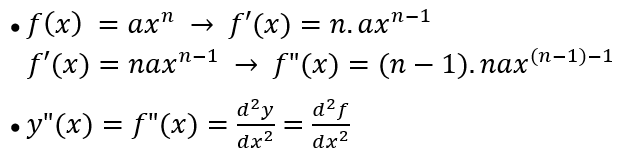
Contoh Permasalahan
1
Carilah turunan kedua dari fungsi fungsi berikut:
- f(x)= 4x³+3x²+12x
- f(x)= 2x⁵-6x³+28x³-54x²
- f(x)= (3x+2)⁵
- f’(x)= 2x²+3x+56x
Penyelesaian:
- Pertama turunkan [f’(x)] persamaan fungsi tersebut → 12x²+6x+12
Lalu untuk mendapatkan persamaan Turunan Kedua perlu menurunkan persamaan tersebut lagi → 24x+6 - Pertama turunkan [f’(x)] persamaan fungsi tersebut → 10x⁴-18x²+84x²-108x²
Lalu untuk mendapatkan persamaan Turunan Kedua perlu menurunkan persamaan tersebut lagi → f’’(x)= 40x³-36x+168x-216x = 40x³+132x-216x - Jika dengan ada persamaan seperti ini f(x)= (bx+c)^a, yang pertama kita lakukan adalah turunkan persamaan tersebut → f’(x) = a(bx+c)^(a-1)×b
dengan adanya rumus ini maka persamaan tersebut akan menjadi seperti ini → f’(x)= 5(3x+2)⁴×3
Ingat, jika diminta untuk dijadikan menjadi Turunan kedua maka hasil persamaan tersebut kita turunkan lagi → f'’(x)= 20(3x+2)³×9 = 180(3x+2)³ - Langsung diturunkan persamaan tersebut menjadi → 4x+3+56 = 4x+59
Pengaplikasian pada kehidupan sehari hari
- Ekonomi dan Bisnis
Turunan kedua berperan penting dalam optimasi, memungkinkan menentukan nilai maksimum dan minimum keuntungan yang didapatkan. - Fisika
Turunan kedua dari fungsi posisi terhadap waktu memberikan informasi mengenai percepatan suatu objek, memungkinkan analisis bagaimana kecepatan berubah seiring waktu. - Turunan kedua membantu dalam menentukan titik suatu fungsi, baik itu nilai maksimum maupun minimum, serta dalam mencapai efisiensi biaya dalam berbagai proyek, seperti menentukan waktu penyelesaian proyek konstruksi dan meminimalkan pengeluaran. Bahkan, konsep ini juga diterapkan dalam menghitung gradien garis singgung pada kurva atau fungsi.
Latihan Soal
Tips Mengerjakan
Perhatikan:
- Gunakan aturan turunan dengan teliti
- Periksa kembali setiap langkah
- Pahami makna matematis dari turunan kedua
- Latih kemampuan dengan berbagai fungsi
- Gunakan kalkulator atau software matematika untuk membantu