Permasalahan Optimum

Aplikasi Turunan dalam Kehidupan Sehari-hari

Kata Pengantar

Pada bagian sebelumnya, kita sudah belajar tentang nilai optimum (nilai stasioner). Ternyata, Kita bisa mengimplementasikan konsep ini pada banyak hal, lho! Pada bab ini, kita akan belajar tentang bagaimana cara mencari nilai optimum pada suatu permasalahan dalam kehidupan nyata. Belum bisa terbayang? Gak apa-apa, ayo kita bahas bersama!

Definisi

Sebelum masuk ke dalam permasalahan nyata, kita akan review sedikit tentang nilai optimum, ya! Nilai optimum adalah nilai maksimum atau minimum yang dimiliki suatu fungsi. Coba kita gambar menggunakan grafik!


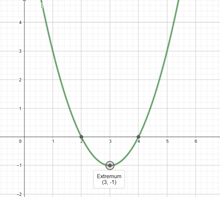
Gambar Grafik


Grafik di atas adalah fungsi f(x)=x²-6x+8. Dari gambar, kita bisa menentukan bahwa titik optimum fungsi tersebut (disebut extremum dalam Bahasa Inggris) adalah titik P(3,-1). Titik tersebut adalah titik minimum dari fungsi f(x). Lalu, apakah fungsi f(x) memiliki nilai maksimum? Jawabannya adalah ya, teman-teman, tetapi koordinatnya tak terhingga. Fungsi inilah yang kita sebut fungsi objektif. Bagaimana kalau kita tambahkan pembatas 1 ≤ x ≤ 4?


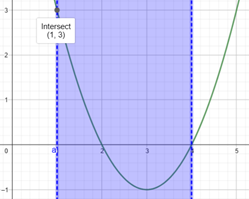
Gambar Grafik


Daerah yang diwarnai biru adalah batas 1 < x > 4. Dari gambar, kita bisa menentukan bahwa titik maksimum dari fungsi f(x), dengan {x | 1 ≤ x ≤ 4, x ∈ R} berada pada R(1,3), sementara titik minimumnya tetap berada pada koordinat (3,-1). Fungsi ini disebut fungsi pembatas. Kemudian, bagaimana jika batas yang ditentukan tidak mencakup titik minimum dari fungsi f(x)? Ayo kita cari tahu!


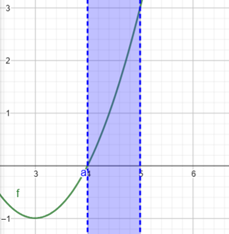
Gambar Grafik


Coba kita lihat contoh lain!


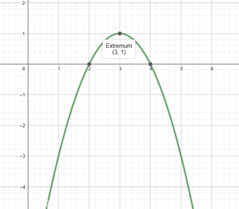
Gambar Grafik


Grafik di atas adalah fungsi g(x)=-x²+6x-8. Dari gambar di atas, kita bisa menentukan bahwa titik optimum fungsi g(x) adalah titik Q(3,1) dan merupakan titik maksimum. Sama seperti fungsi f(x), koordinat titik minimum fungsi g(x) tak terhingga.

Rumus

Sekarang teman-teman sudah paham kan mengenai titik optimum? Lalu, bagaimana cara menentukan titik optimum dari suatu fungsi? Teman-teman dapat menggunakan rumus berikut:
f'(x) = 0
f'(x) merupakan turunan dari fungsi f(x). Dari rumus ini, kita dapat menentukan koordinat x dan y optimum fungsi tersebut.

Contoh Permasalahan

1

Tentukan nilai maksimum dan nilai minimum untuk fungsi f(x) = -x²+2x+8 dalam interval 0 ≤ x ≤ 3.

Penyelesaian:

  • f′(x) = 0
  • −2x + 2 = 0
  • −2x = −2
  • x = 1

  • Selanjutnya substitusi nilai x ke fungsi f(x) untuk menentukan nilai maksimum dan minimumnya.

  • f′(x) = 0
  • x = 1 ⟹ f(x)= −(1)² + 2(1) + 8 = −1 + 2 + 8= −1 + 2 + 8 = 9 = 9 (Maksimum)

  • saat di ujung selang / interval [0,3]

  • x = 0 ⟹ -0² + 2(0) + 8 = 8
  • x = 3 ⟹ f(x) = −3² + 2(3) +8 = −9 + 6 + 8 = 5 (Minimum)
2

Sebuah kapal akan menyelam ke dalam sebuah palung. Palung tersebut menyerupai fungsi y=x^2+2x-4. Jika kapal bergerak dari kedalaman y=4 dengan kapal kecepatan 1satuan/jam, maka berapa lama waktu yang dibutuhkan kapal tersebut hingga mencapai dasar palung?

Penyelesaian:

  • y’ = 2x+2
  • 0 = 2x+2
  • x = -1
  • y= (-1)²+2(-1)-4
  • y= -5

  • Jarak antara kapal dan dasar palung:
  • -5 - 4 = -9 = 9 (jarak tidak ada yang negatif)

  • Mencari waktu:
  • Waktu= Jarak/kecepatan
  • Waktu= 9/1
  • Waktu= 9 jam

Tipe Permasalahan Optimum

1. Masalah Geometri

  • Luas maksimum/minimum
  • Volume maksimum/minimum
  • Keliling minimum

2. Masalah Ekonomi

  • Biaya minimum
  • Keuntungan maksimum
  • Pendapatan optimal

3. Masalah Fisika

  • Jarak minimum
  • Waktu minimum
  • Kecepatan optimal

Latihan Soal

contoh jawaban: x < a atau x > b

  1. Nilai maksimum dan minimum untuk fungsi f(x)= 6x²−x³ pada interval −1 < x < 3 adalah…

  2. Fungsi keuntungan suatu produk adalah P(x) = -x²+100x-2000, dimana x adalah jumlah produk. Tentukan keuntungan maksimum.

  3. Nilai minimum fungsi f(x)=x³-6x²-15x+1 untuk -2 ≤ x ≤ 4 adalah ...

  4. Tingkat popularitas dan dukungan pada seorang calon presiden kuat pada bulan ke-t diasumsikan f (t) persen dari banyaknya pemilih di daerah itu. Andaikan tim sukses merencanakan suatu rumus untuk kaitan antara t dan f pada setiap saat t memenuhi:
    f(x) = -2t²+pt+30+p, 0 ≤ x ≤ 6
    Dengan saat t = 0 (saat proses pemilihan dimulai) besarnya tingkat popularitas dan dukungan pada calon kuat ini pada bulan kedua adalah (5p-2)% dari pemilih. Tingkat popularitas calon kuat ini maksimum pada bulan ke-t, dengan t memenuhi?

  5. gambar soal5
    Seseorang akan mendaki sebuah bukit yang memiliki dua puncak. Bukit tersebut berbentuk seperti fungsi y=4x²-2x⁴. Tentukan berapa jarak terdekat antara puncak 1 dan puncak 2!



Kirimkan pesan untuk tanya pembahasan.

Bu Fitri Bu Byas Bu Uut Bu Lewi Bu Iswari

Tips Mengerjakan

Perhatikan:

  • Pastikan semua informasi penting sudah diidentifikasi
  • Gunakan variabel yang tepat dan konsisten
  • Perhatikan satuan dalam soal
  • Periksa kembali apakah hasil masuk akal
  • Uji nilai di sekitar titik kritis