Titik Stasioner

Konsep Dasar dan Aplikasi dalam Kalkulus

Kata Pengantar

Pada materi sebelumnya kita sudah belajar tentang fungsi naik dan fungsi turun dalam Turunan Fungsi Aljabar, selanjutnya kita akan mempelajari Titik Stasioner. Dalam materi ini, kita akan membahas definisi titik stasioner, rumus titik stasioner, contoh soal dan pembahasan, serta aplikasi titik stasioner dalam kehidupan sehari-hari. Semoga materi ini bermanfaat dan membantu dalam memahami materi titik stasioner ini. Sung ae kita mulai!!!

Jika f'(x) = 0 dari fungsi f(x), nilai f(x₀) disebut nilai stasioner dan titik (x₀, f(x₀)) disebut titik stasioner.

Rumus Turunan Fungsi Stationer

f'(x)=0
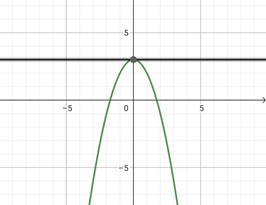
gambar grafik
Garis hijau menunjukkan kurva suatu fungsi dan garis hitam merupakan titik stasioner dari turunan fungsi suatu kurva.

Jenis-jenis Titik Stasioner

Uji Turunan Pertama

Jika f'(c) = 0, maka f(c) adalah nilai stasioner f pada x = c. Nilai stasioner mungkin saja merupakan nilai balik maksimum, nilai balik minimum, atau titik belok horizontal pada grafik fungsi f. Jenis nilai-nilai stasioner ini dapat ditentukan dengan memperhatikan tanda kepositifan f'(x) di sekitar x = c.


1. f(x) mempunyai nilai balik maksimum f(c) jika f'(x) berganti tanda dari positif menjadi negatif saat melalui nol.


2. f(x) mempunyai nilai balik minimum f(c) jika f'(x) berganti tanda dari negatif menjadi positif saat melalui nol.


3. f(x) mempunyai titik belok horizontal pada c jika f'(x) tidak berganti tanda saat melalui nol.

Uji Turunan Kedua (f"(x))

Uji Turunan kedua digunakan untuk menyatakan kecekungan atau menentukan titik belok kurva pada suatu fungsi.


1. Jika f”(a) < 0, maka f(a) adalah nilai balik maksimum fungsi f.


2. Jika f”(a) > 0, maka f(a) adalah nilai balik minimum fungsi f.


3. Jika f”(a) = 0, maka f(a) bukan nilai stasioner fungsi dan titik (a, f(a)) adalah titik belok kurva fungsi f.

Video Seru!

Contoh Soal

Soal 1:

Tentukan titik stasioner dari fungsi di bawah ini

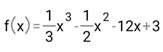
contoh soal

untuk menjawab soal diatas kita harus menurunkan fungsi nya terlebih dahulu
f’(x) = x² - x - 12
kemudian gunakan rumus turunan fungsi stasioner
f’(x) = x² - x - 12
f’(x) = 0
(x+3)(x-4) = 0
x = -3 v x = 4
setelah mendapatkan nilai x nya, maka kita masukkan x ke dalam f(x) untuk mendapatkan titik y-nya

untuk x = -3
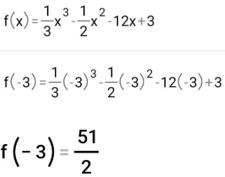
jawaban

untuk x = 4
jawaban
Titik stasioner yang kita dapatkan yaitu (-3,51/2) dan (4,-95/3).

Soal 2:

fungsi y = x³ – 6x² + 12x + 1 mempunyai nilai stasioner...


f’(x) = y’ = 0
3x² - 12x + 12 = 0
3(x-2)² = 0
x = 2


masukan nilai x ke dalam fungsi y untuk memperoleh nilai stasioner (y)

f(2)=(2)³-6(2)²+12(2)+1 f(2)=8-24+24+1 f(2)=9


Jadi, nilai stasioner fungsi tersebut adalah y=9.

Soal 3:

soal


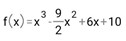
f’(x)=0
3x²-9x+6=0
3(x-1)(x-2)=0
x=1vx=2


untuk menentukan nilai maksimum kita harus menggunakan turunan kedua.


f”(x)=6x-9

akan memiliki nilai maksimum apabila f”(x)≺0 lalu masukkan nilai x ke dalam turunan kedua


f”(x)=6(1)-9= -3
f”(x)=6(2)-9= 3


Karena f”(1)≺0 maka berarti nilai fungsi f mencapai maksimum saat nilai x=1

Soal 4:

Koordinat titik belok fungsi f(x)= x³-3x²+6x+8 adalah…


f”(x)=0
merupakan titik belok fungsi, sehingga
f’(x)= 3x²-6x+6
f”(x)=6x-6
f”(x)=0
6x-6=0
6x=6
x=1


lalu masukkan nilai x ke fungsi f(x)


f(1)=(1)³-3(1)²+6(1)+8
f(1)=12


Jadi, koordinat titik beloknya adalah (1,12).

Soal 5:

Fungsi f(x)= 2x²-16x mempunyai titik...

f’(x)=0
4x-16=0
4x=16
x=4


masukkan nilai x ke dalam fungsi


f(4)=2(4)²-16(4)
f(4)=32-64
f(4)=-32


untuk mencari titik maksimum atau minimum maka kita harus mencari turunan kedua f”(x)=4 jika f”(x)>0 maka titik baliknya minimum


Jadi, fungsi f(x)= 2x²-16x memliki titik minimum (4,-32).

Aplikasi Titik Stasioner

  1. Ekonomi dan Bisnis
    Konsep ini membantu memaksimalkan keuntungan dan meminimalkan biaya.
  2. Teknik dan Desain
    Insinyur menggunakannya untuk meningkatkan efisiensi mesin serta stabilitas struktur.
  3. Fisika
    Titik stasioner membantu menentukan kecepatan maksimum dan optimasi energi.
  4. Pertanian dan Lingkungan
    Memanfaatkannya untuk mengoptimalkan hasil panen dan pengelolaan sumber daya.
  5. Kesehatan
    Titik stasioner digunakan untuk menentukan dosis obat optimal dan menganalisis denyut jantung.
  6. Keuangan dan Investasi
    Konsep ini membantu trader dalam menganalisis pergerakan harga saham.
  7. Transportasi dan Logistik
    Titik stasioner digunakan dalam perencanaan rute optimal untuk efisiensi perjalanan.

Latihan

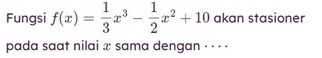
  1. latsol 1

  2. Fungsi f(x) = 2x³-9x²+12x+1 akan mencapai minimum pada saat nilai x = …

  3. 3. Fungsi f(x) = -x²+4x-1 mempunyai titik… (maksimum/minimum/belok)

  4. Fungsi f(x) = x²-4x+3 mempunyai titik… (maksimum/minimum/belok)

  5. Titik stasioner dari fungsi f(x) = 2x³-3x²-12x+4 adalah...

  6. latihan 6

  7. Titik stasioner dari fungsi f(x) = x³-3x+3 adalah…



Kirimkan pesan untuk tanya pembahasan.

Bu Fitri Bu Byas Bu Uut Bu Lewi Bu Iswari

Catatan Penting

  • Tidak semua titik dengan f'(x) = 0 adalah titik ekstrim
  • Perlu memeriksa f''(x) untuk menentukan jenis titik stasioner
  • Titik stasioner bisa terjadi di beberapa titik dalam satu fungsi
  • Fungsi kontinu belum tentu memiliki titik stasioner